Introduction

Recently, I came across a very interesting problem in an online forum that deals with streams of objects having a natural order (think comparable types in Go or C#’s IComparable<T>, etc)

I had the opportunity to brainstorm a solution and am enthusiastic to share it with the community.

Imagine having two streams, containing such comparable objects originating from two sources. In the scenario, the sources are homogeneous but distributed and there is need to compute summary statistics from the aggregate of the two.

While there are the multiple important metrics that can give insight into the data, one such important metric is the median, which divides the population of sample points into symmetrical halves.

This kind of “sub-problem”, let’s assume, frequently arises in the context of sensor networks, search engines, sequence alignment in bioinformatics, etc.

The question is framed as follows: given two sorted lists S and B of sizes N1 and N2, the problem is to efficiently find the median of the combined list without explicitly merging them.

Philosophy

One thing we can do is merge the two lists, sort them and then compute the median from the middle indices. But each step in that pipeline does a lot of work - in total O(N1+N2) + O((N1+N2) x log2(N1+N2))!

Can we think a little deeply, may be, creatively use the mathematical properties of ‘sorted collections’ and avoid doing the expensive intermediate work? Let’s find that out.

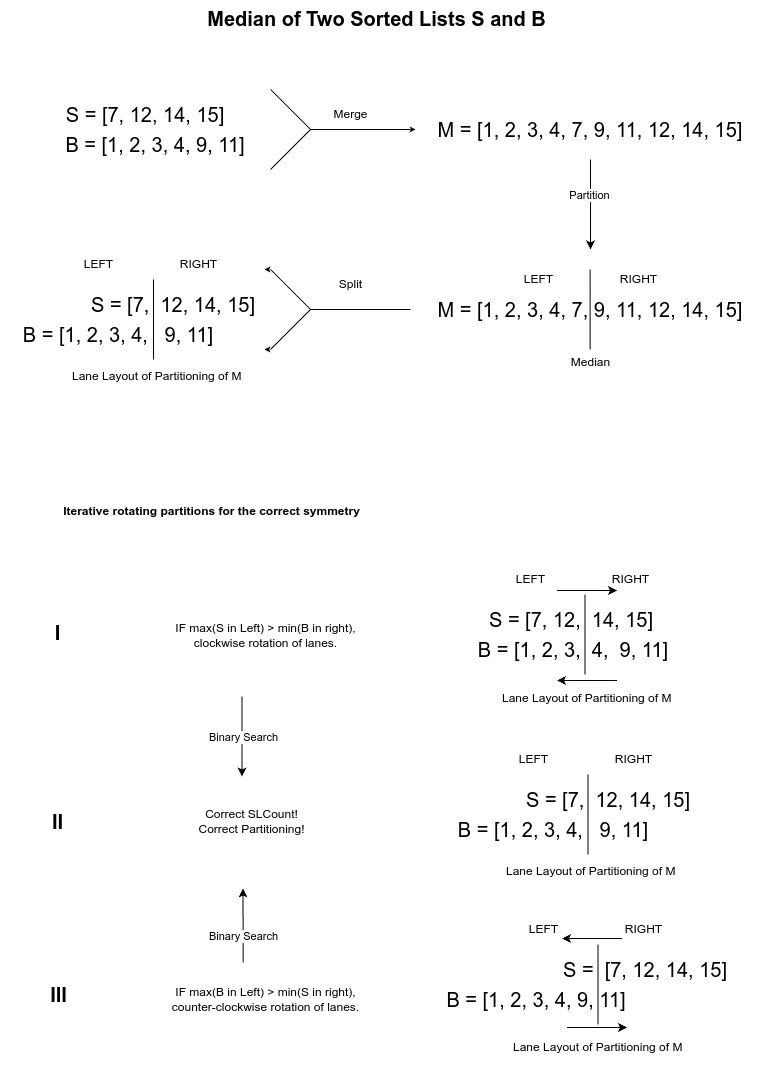
First let’s assume the two lists are merged into a ghost array, M. Then we will map the observations from M onto our two separate sorted arrays S and B and find one-to-one correspondences between the two layouts.

In M, the median divides the population into a symmetry of equal populations: the left half has all elements lesser than that of the right half.

Assume M is written out on a single line in a sorted order, and then draw a vertical “divider” line between the two populations, to partition them.

Now we are going to rearrange the line into two lines stacked on top of each other while keeping the divider line intact, such that each of those lines represent S and B, with S in top and B in bottom. While doing this, keep in mind to maintain the sorted order of S and B respectively. Let’s call this picture, the ’lane layout of partitioning of M’.

This rearranged drawing illustrates S and B’s contributions to the left partition and the right partition of the ghost merged array M.

The facts are:

1. Each element on the left partition is lesser than all of those in the right partition.
2. Count of total elements on the left partition is equal to that in the right partition due to the median, and it is constant, say L.

Now our questions are:

1. How many and which contributions from S went into the left and right partitions of the ghost array M?
2. How many and which contributions from B went into the left and right partitions of the ghost array M?

Let’s try to use the facts to arrive at the answers to the above questions.

We know the array sizes N1 and N2, and that the partition sizes are constant and equal, L.

If S contributed SLCount items to the left partition of M, then S’s contribution to the right partition is N1 - SLCount. Then, since left partition size is L, B will have to contribute “L - SLCount” items to the left partition to maintain its size invariant. Also, then B will contribute N2 - (L - SLCount) items to the right partition of M.

So! Just by playing detective with the number SLCount, we can derive the other numbers of questions 1 and 2 and have indirectly arrived at the partitioning.

Computing the median, once we have the correct partitions, is easy. If M is evenly sized, take the max from the left partition and the min from the right partition, and average the two. If M has odd count, and assuming in the rearrangement of M into S and B, we kept the higher contribution counts of each on the left partition, then median is simply the max of the left partition.

Therefore, the game is find out how many elements S contributed in the left partition of M, and the rest of the observations follow from the facts.

We can exploit another property of sorting in this game. If we were to do trial-and-error starting from 0 counts of S to whole of S to determine SLCount, we are looking at a linear time computation. Instead, since S is sorted, possibly we can use binary search to determine the correct SLCount? Let’s bound the SLCount into a range, lowSLCount = 0 and HighSLCount = size of S, which is N1. We are going to narrow down to a number between 0 and N1 using binary search. For starters, let’s take the average of lowSLCount and HighSLCount as testSLCount. The search space for testSLCount will narrow down as we test exit conditions. How would we know which SLCount is correct? For that we need to go back to our partitioning picture of M, and derive the exit conditions.

In the ’lane layout of partitioning of M’, we know that all elements of S lane on the left partition are smaller that all elements of S lane on the right partition. Similarly, all elements of B lane on the left partition are smaller that all elements of B lane on the right partition. Therefore, the intra-lane ordering is intact.

However, if we prove cross-lane ordering across the divider line from S and B, then we will have successfully proven that the left and right partitions are correct, therefore SLCount is the correct number. I will leave you to brainstorm that fact.

There’s an easy way to do so: Find the max of S’s contributions in the left partition and test if it is less than the min of B’s contributions in the right partition. And, the max of B’s contributions in the left partition and test if it is less than the min of S’s contributions in the right partition. If for a particular SLCount, if the above two tests pass, then we have found the correct partitioning and hence, SLCount!

What if either of the tests fail? If max(S in Left) > min(B in right), then we must take lesser contributions from S and more contributions from B. I call this the clockwise rotation of ’lane layout of partitioning of M’. Reduce the search space to lowSLCount = 0 and HighSLCount = testSLCount - 1, since testSLCount must be lesser than its current value. If max(B in Left) > min(S in right), then we must take higher contributions from S and reduce contributions from B. I call this the counter-clockwise rotation of ’lane layout of partitioning of M’. Reduce the search space to lowSLCount = testSLCount + 1 and HighSLCount = N1, since testSLCount must be higher than its current value.

Diagram

The following diagram illustrates a numerical example of the algorithm. The layout and rotations should drive home the ideas outlined in the explanation above:

Code

The code for the above algorithm in C#, is below:

using static System.Math;

public class MedianOfTwoSortedArraysSolution
{
    public double FindMedianSortedArrays(int[] nums1, int[] nums2)
    {
        // S = Smaller array
        // B = Bigger array
        var (S, B) = nums1.Length <= nums2.Length ? (nums1, nums2) : (nums2, nums1);

        // Let M be the merged array = [..S, ..B]
        // Size of merged array is
        int MSize = S.Length + B.Length;

        // IMPORTANT: Median finding logic depends on whether M has even or odd count of elements
        bool isEven = MSize % 2 == 0;

        // INVARIANT: The median of the merged array divides it into a one and only one correct symmetry:
        //      50% count on the left partition and 50% on the right partition;
        // if isEven, then M == LeftPartitionSize x 2 (due to integer division),
        //      else !isEven, then M == LeftPartitionSize x 2 - 1 (M + 1 is even)
        //      so for odd sized M, LeftPartitionSize = RightPartionSize + 1, this influences the formula for
        //      finding median for odd sized M
        int LEFTPARTITIONSIZE = (MSize + 1) >> 1; // CONSTANT
        
        // Binary search to find the correct element count from S (left partition of S) 
        //      which goes into the left partition of M
        // Let SLCount = correct number of elements from S (left partition of S) 
        //      which goes into the left partition of M
        // Then BLCount = correct number of elements from B (left partition of B) 
        //      which goes into the left partition of M
        // Lemma: LeftPartitionSize (INVARIANT) = SLCount + BLCount;
        // Binary search to determine correct SLCount, over the smaller array to reduce time complexity
        int lowerBoundSLCount = 0, upperBoundSLCount = S.Length;

        while (lowerBoundSLCount <= upperBoundSLCount)
        {
            // Test element counts (also partition boundaries) of both S and B
            //      which goes into LeftPartition of M
            int testSLCount = (lowerBoundSLCount + upperBoundSLCount) >> 1;
            int testBLCount = LEFTPARTITIONSIZE - testSLCount;

            // Values for the above element counts
            int SLMAX = int.MinValue, BLMAX = int.MinValue;
            int SRMIN = int.MaxValue, BRMIN = int.MaxValue;

            // testSLCount is size, hence rightmost value in the Left Partition of S has index testSLCount - 1
            // Guard for
            if (testSLCount - 1 >= 0) SLMAX = S[testSLCount - 1];
            // Hence, leftmost value in the Right Partition of S has index testSLCount
            // Guard for
            if (testSLCount < S.Length) SRMIN = S[testSLCount];
            // testBLCount is size, hence rightmost value in the Left Partition of B has index testBLCount - 1
            // Guard for
            if (testBLCount - 1 >= 0) BLMAX = B[testBLCount - 1];
            // Hence, leftmost value in the Right Partition of B has index testBLCount
            // Guard for
            if (testBLCount < B.Length) BRMIN = B[testBLCount];

            // Binary search logic for the correct SLCount
            //      (and therefore, BLCount which is LEFTPARTITIONSIZE - SLCount)
            
            /* 
             * Iteration of partitionings to find the correct symmetry:
             * Rotate top (small) and bottom (big) arrays to arrive at the correct partitioning
             *      S0, S1, S2 ... S[testSLCount - 1] or SLMAX | SRMIN or S[testSLCount], S[testSLCount + 1], ... S[S.Length - 1]
             * B0, B1, B2, ....... B[testBLCount - 1] or BLMAX | BRMIN or B[testBLCount], B[testBLCount + 1], ...... B[B.Length - 1]
             */
             
            if (SLMAX <= BRMIN && BLMAX <= SRMIN)
            {
                return isEven ? CalculateMedian(SLMAX, BLMAX, SRMIN, BRMIN) : CalculateMedian(SLMAX, BLMAX);
            }

            // Counter Clockwise rotation, take higher count of elements from S and
            //      take lower count of elements from B to maintain Left Partition Size invariant and
            //      to maintain sorted order of M
            else if (BLMAX > SRMIN) lowerBoundSLCount = testSLCount + 1;
            // Clockwise rotation, take lower count of elements from S and
            //      take higher count of elements from B to maintain Left Partition Size invariant
            //      to maintain sorted order of M
            else if (SLMAX > BRMIN) upperBoundSLCount = testSLCount - 1;
        }

        // This case is never executed.
        return 0.0;
    }

    /// <summary>
    /// Calculate median of combined array M from S and B, when M.Length is even.
    /// </summary>
    /// <param name="SLMAX"></param>
    /// <param name="BLMAX"></param>
    /// <param name="SRMIN"></param>
    /// <param name="BRMIN"></param>
    /// <returns> A double valued median of combined array M from S and B, when M.Length is even.</returns>
    private static double CalculateMedian(int SLMAX, int BLMAX, int SRMIN, int BRMIN) 
        => (Max(SLMAX, BLMAX) + Min(SRMIN, BRMIN)) / 2.0;

    /// <summary>
    /// Calculate median of combined array M from S and B, when M.Length is odd.
    /// </summary>
    /// <param name="SLMAX"></param>
    /// <param name="BLMAX"></param>
    /// <param name="SRMIN"></param>
    /// <param name="BRMIN"></param>
    /// <returns> A double valued median of combined array M from S and B, when M.Length is odd.</returns>
    private static double CalculateMedian(int SLMAX, int BLMAX) 
        => Max(SLMAX, BLMAX);

}

Conclusion

Eventually, this process is guaranteed to converge to the correct SLCount, since a partitioning of M always exists! The binary search on the smaller list ensures that the partitioning check runs in O(log(min(N1,N2))) time complexity, reducing overhead compared to direct merging.

If you are with me so far, thanks for reading!