Quadratic Forms and Linear Systems

Many important quantities arising in engineering are mathematically modelled as Quadratic Forms. Output noise power in Signal Processing, Kinetic and Potential Energy functions in Mechanical Engineering, Covariance Models of Random Variable Linear Dependence and Principal Component Analysis in Statistics, etc. are some of the frequently occurring applications of Quadratic Forms, illustrating their ubiquity and importance.

A Quadratic Form \(f(x)\) on \(\mathbb{R}^n\) is a function \(f : \mathbb{R}^n \rightarrow \mathbb{R}\) such that:

The graph of a positive-definite convex quadratic form is a hyperparaboloid in \(\mathbb{R}^{n + 1}\) dimensions.

Frequently, in many applications, we are interested in minimizing the quadratic form \(f(x)\), for example, minimising the energy function of a mechanical system so that it is in a stable state.

Suppose that, we have at our hands, a quadratic form obtained by mathematically modelling some quantity of interest and we wish to minimize it. At the minimum point \(\mathbf{x}^*\) (henceforth referred to as the minimizer), the gradient \(\nabla : \mathbb{R}^n \rightarrow \mathbb{R}\) of a function \(f(x)\) is always zero by first order optimality condition. Hence,

At \(\mathbf{x}^*\), \(\nabla f(\mathbf{x}^*) = 0 \implies H \mathbf{x}^* + \mathbf{c} = 0 \text{ or } H \mathbf{x}^* = -\mathbf{c}\).

Thus, finding the minimum of the quadratic form \(f(\mathbf{x})\) is equivalent to solving the linear system \(H \mathbf{x}^* = -\mathbf{c}\) for the unknown \(\mathbf{x}^*\).

Again, suppose that we have at our hands a one-dimensional two-point boundary value problem (BVP), for example, the governing equations of flow of heat in a thin conducting rod with a source (\(t\) is the continuous 1D spatial domain, \(x\) is the temperature, \(g(t)\) is the heat source):

If we discretise the domain and convert the above differential equation to a finite difference equation, we obtain a linear system \(H \mathbf{x} = - \mathbf{c}\), where the temperatures \(\mathbf{x}\) can be a very high dimensional vector due to the underlying problem being continuous. The \(H\) represents the second-order derivative operator \(\frac{d^2 x}{dt^2}\) and \(- \mathbf{c}\) the heat source in the discretised domain \(\mathbf{R}^n\).

Since the BVP is continuous, the discretisation \(x\) is made high-dimensional to capture its fidelity; therefore the matrix \(H \in \mathbb{R}^{n \times n}\) is very large. More importantly, due to the structure and regularity of the 2^nd order finite difference operator, we can make the following qualifiers: the matrix \(H\) is sparse, symmetric and positive definite. Solving such a large linear system with a direct matrix factorisation method is prohibitively expensive (of the order of \(\mathcal{O}(\frac{2}{3} n^3)\)). Hence, a better alternative is to solve the system iteratively and reach a solution in \(r << n\) steps that is close enough to the actual solution, which will cost us much less than a direct method.

One idea to solve the linear system \(H \mathbf{x} = - \mathbf{c}\) is to use a stationary method, such as Jacobi or Gauss-Seidel. However, there is no guarantee of convergence, even for positive definite matrices.

A better approach is to utilize the observation made earlier: convert the linear system to its dual quadratic form and apply an iterative optimisation process on the objective function!

At the minimum of \(f(\mathbf{x})\), we would have found the solution to our original linear system.

We can summarise this section by making the following statement [See PCG Appendix C1 for proof]:

Line Search Techniques

Now that we have our objective function, namely the quadratic form \(f : \mathbb{R}^n \rightarrow \mathbb{R}\), our goal is to minimise it. We formalise our unconstrained optimisation problem \(\text{(P)}\) as:

Before we begin, let us introduce some definitions:

1. Error at the i-th iterate: \(\mathbf{e}_i = \mathbf{x}_i - \mathbf{x}^*\)
2. Residual at the i-th iterate: \(\mathbf{r}_i = H \mathbf{x}_i + \mathbf{c}\), from linear system perspective.
3. Gradient at the i-th iterate: \(\nabla f(\mathbf{x}_i) = H \mathbf{x}_i + \mathbf{c}\), from objective function perspective.

We notice that:

1. \(\mathbf{r}_i = H \mathbf{x}_i + \mathbf{c} = H \mathbf{x}_i - H \mathbf{x}^* = H (\mathbf{x}_i - \mathbf{x}^*) = H \mathbf{e}_i\), that is, the residual is simply the error mapped from the domain of \(H\) to the range of \(H\).
2. The Residual of the Linear System is equal to the Gradient of the Objective Function. Throughout the article, whenever we mention residual, we also mention gradient to reinforce this fact.
3. Since \(\mathbf{x}^*\) is unknown, \(\mathbf{e}_i\) is unknown at every step, but the residuals \(\mathbf{r}_i\) are always known. So whenever we want to use the error, we can simply work with the residual in the rangespace of \(H\).

Now comes the core philosophy of Line Search: given our objective function \(f(\mathbf{x})\), we start with an initial guess \(\mathbf{x}_0\), and iterate our way downhill on \(f(\mathbf{x})\) to reach \(\mathbf{x}^*\). At any i-th iterate, we are at the point \(\mathbf{x}_i\), and to travel to our next point \(\mathbf{x}_{i + 1}\), we must choose a direction of descent \(\mathbf{p}_i\), and then move a step length \(\alpha_i\) the right amount so that along this direction, \(f(\mathbf{x}_{i + 1}) = \phi(\alpha_i)\) is minimum. Mathematically,

One approach is to use the Steepest Descent (SD) technique to compute and move along a direction \(\mathbf{p}_i\) towards vanishing gradient:

SD moves along (or opposite to be precise) the residual/gradient vector at each iterate. One fact we state without proof [see PCG pg. 6; can be derived from 1D calculus] is that the residual/gradient at the current iterate i is always orthogonal to the previous residual/gradient at i - 1.

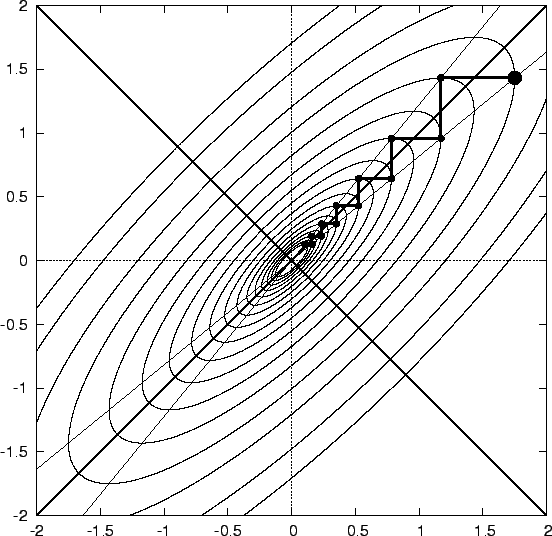
As can be seen from the above picture, this is unfortunate, because we repeat directions in multiple steps a lot, and the number of steps needed to converge to the minimum point \(\mathbf{x}^*\) is extraordinarily large. This could have been avoided if, after taking a new direction each time, we had travelled just the right amount of length in that direction so that in our future march downhill, we never need to step in that direction again.

This raises an important question: If we picked a direction and took the RIGHT step length along it to avoid repeating it, in how many steps will be reach the minimizer \(\mathbf{x}^*\)?

The answer is: n steps! (the dimension of the vectorspace). To see why it is so, we need to wait for some more explanations.

Let us the explore the above idea a bit further in the following sections.

Coordinate Descent Method

To demonstrate the idea of n-directions, let us solve two problems and analyse their solutions. As a first attempt, we will pick the coordinate axes (i.e. the canonical basis) as the directions of descent.

Descent along Conjugate Directions: A Powerful Line Search Method

Two vectors, \(\mathbf{p}_i\) and \(\mathbf{p}_j\) are said to be H-conjugate with respect to some symmetric, positive definite matrix \(H\), if they satisfy,

\begin{align*} \mathbf{p}_i^T H \mathbf{p}_j = \left\{ \begin{array}{ll} \text{ non-zero } & \mbox{if } i = j \\ 0 & \mbox{if } i \neq j \end{array} \right. \: \forall \: i, j \: \in \: [1 \dots n] \\ \end{align*}

From the discussion in the previous section, we outline our goals and issues for the rest of the article as follows:

1. Find a set of n linearly independent set of H-conjugate directions \(\mathbf{p}_i\).
2. Establish relationships between residuals/gradients, search directions and the vectorspace of our solution \(\mathbf{x}^*\).
3. Use the above two rules to calculate the step lengths \(\alpha_i\) along \(\mathbf{p}_i\).

To repeat, we are solving the unconstrained optimisation problem:

The minimiser of our problem \(\text{(P)}\) can be stated as:

Our one-line iterative procedure is:

Now we will slowly build up our procedure, step by step.

Recall that we want to make residual/gradient at the next iterate \(i + 1\) orthogonal to our direction at the current iterate \(i\).

Note that the error at the next iterate is H-conjugate to the previous direction. We will have more to say about this later.

Using our definitions, we have:

Substituting in the previous equation, we get:

All of the terms in the right hand side of the above expression are known at the current iterate. This gives us our step length \(\alpha_i\), our goal #3!

Okay, we admit that it was arbitrary. Why should us wanting to orthogonalise the next residual to the current search direction give us a credible answer for the step length? So, let us try something else: given that we are standing at \(\mathbf{x}_i\), we want to minimise our objective \(f(\mathbf{x})\) at \(\mathbf{x}_{i + 1} = \mathbf{x}_i + \alpha_i \mathbf{p}_i\) over the direction \(\mathbf{p}_i\) (assume it is somehow already calculated). So, we can write:

Now comes our calculus attack: we will differentiate \(\phi(\alpha_i)\) with respect to \(\alpha_i\) and set the derivative to zero to find the directional minimum (Why? Because we know \(\mathbf{x}_i\), we assumed that we already know \(\mathbf{p}_i\), and we just need to find the minimum along this direction)

which is nothing but (see definitions in Section II):

We have now arrived at the same step length as when we arbitrarily forced the next residual to be perpendicular to the current direction. Now, we know better: this step length actually minimises our objective along the current direction, and the former fact just comes about as a corollary! Further, we note that \(\mathbf{r}_{i + 1} \perp \mathbf{p}_i \implies \mathbf{p}_i^T \mathbf{r}_{i + 1} = \mathbf{p}_i^T H \mathbf{e}_{i + 1} = 0\), that is, direction - residual orthogonality implies direction - error H-conjugacy. In fact, we will make the following hand-waving argument: since the error at the next iterate is always H-conjugate to the current search direction, the current search direction is H-conjugate to all the previous search directions, and we don't ever step into a previously encountered direction again in the future, the next error is evermore H-conjugate to all the previous search directions by recursion. Which implies the residual is orthogonal to all the previous search directions! The rigorous proof of this statement is contained in the Expanding Subspace Minimization Theorem, which is presented in the next section.

Before we march ahead, let us establish a relationship between the residuals. We shall use this later in proving some theoretical guarantees. Using our error relationship, premultiply both sides of the equation by \(H\):

Next, we will try to find the directions \(\mathbf{p}_i\). Let us pick, from our available knowledge, n linearly independent vectors \(\{ \mathbf{u}_0, \mathbf{u}_1, \dots, \mathbf{u}_{n - 1} \}\), which we will call as the generator vectors. The easiest choice we can make is the coordinate axes, \(\{ \mathbf{e}_1, \mathbf{e}_2, \dots, \mathbf{e}_n \}\). To construct \(\mathbf{p}_i\), we will take each generator \(\mathbf{u}_i\) and peel off any components that are not H-conjugate to the entire set of previous \(i - 1\) \(\mathbf{p}\) vectors. To kickstart the process, set \(\mathbf{p}_0 = \mathbf{u}_0 = \mathbf{e}_1\) and for all \(i > 1\), iterate as:

To calculate the \(\beta_{ik}\) factors, we exploit the H-conjugacy property of \(\mathbf{p}_i\) directions. Transpose above equation and post-multiply with \(H \mathbf{p}_j, j \in [0, \dots, i - 1]\):

Unfortunately, this means that to calculate each \(\mathbf{p}_i\) upto the n-th direction, all the previous \(H \mathbf{p}_j, j \in [0, \dots, i - 1]\) directions must be kept in storage. This is not very efficient. In fact, the total cost of generating all the search directions is \(\mathcal{O}(n^3)\)), making direct factorisation look appealing! This brings us to the topic of our next section: Conjugate Gradients (or Conjugate(d) Gradients / Conjugate(d) Residuals), a very efficient method of constructing Conjugate Directions.

But wait! Did we not mention before, this conjugate directions process will guarantee convergence in n-steps? Or will it, really? It sounds quite arbitrary. Are we full of ourselves? Why should it happen at all? Let's attack this notion with a mathematical analysis!

We will try to do this: first we will assume that the process indeed converges in n-steps, which implies, the initial error term \(\mathbf{e}_0\) is made up of n-vectors oriented along these directions \(\mathbf{p}_i\). Then, we shall use the H-conjugacy properties of the directions. If we find that, \(\mathbf{e}_n\), that is error after n-steps, is not zero, our big claim is grossly incorrect, and we will terribly fall from grace. However, if \(\mathbf{e}_0\) is indeed zero, we would have proven our n-step convergence assumption on stone and are right on target!

Without much ado, let's formulate the math:

Premultiplying \(\mathbf{p}_k^T H\) and exploiting H-conjugacy, \(\mathbf{p}_k^T H \mathbf{p}_j = 0 \: \forall \: k \neq j\) :

Using the fact that \(\sum_{i = 0}^{k - 1} \: \alpha_i \mathbf{p}_k^T H \mathbf{p}_i = 0\),

We also know that, \(\mathbf{e}_{i + 1} = \mathbf{e}_i + \alpha_i \mathbf{p}_i\) or \(\mathbf{e}_k = \mathbf{e}_{k - 1} + \alpha_{k - 1} \mathbf{p}_{k - 1}\). Recursively expanding this formula into a summation, we get, \(\mathbf{e}_k = \mathbf{e}_{k - 1} + \alpha_{k - 1} \mathbf{p}_{k - 1} = \mathbf{e}_0 + \sum_{i = 0}^{k - 1} \: \alpha_i \mathbf{p}_i\). Substituting this into the above expression:

This means:

Moving ahead,

Substituting \(k = n\),

because we do not have any directions beyond the (n - 1)-th iterate.

Therefore, the error at the n-th step is really zero, and we have arrived at this conclusion by just using the H-conjugacy property! Thus, we can safely state that this Conjugate Directions method indeed converges in n-steps, as we have been advertising. (Disclaimer: The problem has to be convex quadratic positive-definite!)

Okay, now we can move forward to the next sections in confidence and peace of mind.

Some Proofs on our Road to Enlightenment

Conjugate Gradients: A Method of Conjugate Directions

All of our machinery is in place now. We collect the necessary facts in an iterative loop; the simplicity and terseness of the algorithm completely belies the conceptual buildup we went through in the previous sections. So, without any further ado, let's present the Conjugate Gradient algorithm in one piece now.

1. Given, \(\mathbf{x}_0\).
2. Set \(\mathbf{r}_0 \leftarrow H \mathbf{x}_0 + \mathbf{c}\), \(\mathbf{p}_0 \leftarrow - \mathbf{r}_0\) and \(i \leftarrow 0\).
3. while \(\lVert \mathbf{r}_i \rVert_2 \neq 0\), do:
4. Step Length:

\begin{align*} \alpha_i = \frac{\mathbf{r}_i^T \mathbf{r}_i}{\mathbf{p}_i^T H \mathbf{p}_i} \\ \end{align*}

5. Next Iterate:

\begin{align*} \mathbf{x}_{i + 1} = \mathbf{x}_i + \alpha_i \mathbf{p}_i \\ \end{align*}

6. Next Residual:

\begin{align*} \mathbf{r}_{i + 1} = \mathbf{r}_i + \alpha_i H \mathbf{p}_i \\ \end{align*}

7. Direction Update Factor:

\begin{align*} \beta_{i + 1} = \frac{\mathbf{r}_{i + 1}^T \mathbf{r}_{i + 1}}{\mathbf{r}_{i}^T \mathbf{r}_{i}} \\ \end{align*}

8. Next Direction:

\begin{align*} \mathbf{p}_{i + 1} = - \mathbf{r}_{i + 1} + \beta_{i + 1} \mathbf{p}_i \\ \end{align*}

9. Loop Counter Update:

\begin{align*} i \leftarrow i + 1 \\ \end{align*}

10. end while

Computational Complexity:

The dominant costs of the above algorithm is in the Matrix-Vector multiplication step: \(H \mathbf{p}_i\).

For a dense matrix \(H\), the Matrix-Vector multiplication costs, with \(H \rightarrow n \times n\) and \(\mathbf{p}_i \rightarrow n \times 1\), \(\mathcal{O}(n^2)\).

For a sparse matrix \(H\), Matrix-Vector multiplication costs, \(\mathcal{O}(m)\), where \(m\) is the non-zero elements in \(H\).

If we want the initial residual \(H \mathbf{r}_0\) to decrease by a factor \(\epsilon\), say:

\(\| \mathbf{r}_k\| \leq \epsilon \| \mathbf{r}_0 \|\), where \(\mathbf{r}_k\) and \(\mathbf{r}_0\) are the residuals in the \(k^{th}\) and the \(0^{th}\) iterations, then the Number of Iterations, \(n_{iter}\) required for the following algorithms are:

Steepest Descent: \(n_{iter} \leq \frac{1}{2}\mathcal{K}\ln{\frac{1}{\epsilon}}\).

Conjugate Gradient \(n_{iter} \leq \frac{1}{2}\sqrt{\mathcal{K}}\ln{\frac{2}{\epsilon}}\).

where,

\(\mathcal{K}\) is the condition number of \(H\).

If we have a \(d\)-dimensional domain, to solve the boundary value problem, the condition number \(\mathcal{K}\) of the matrix, obtained by discretizing the second order elliptic boundary value problem, is of the order \(\mathcal{O}(n^\frac{2}{d})\), and the number of non-zero entries is of \(\mathcal{O}(n)\).

The Time Complexities for the two methods in this problem are as:

Steepest Descent: \(\mathcal{O}(m\mathcal{K})\)

Conjugate Gradient: \(\mathcal{O}(m\sqrt{\mathcal{K}})\)

For a 2D problem and \(m\) \(\epsilon\) \(\mathcal{O}(n)\), we have the following:

S.D: Time complexity: \(\mathcal{O}(n^2)\)

C.G: Time complexity: \(\mathcal{O}(n^\frac{3}{2})\)

Both methods have a space complexity of \(\mathcal{O}(m)\).

Convergence of CG:

In exact arithmetic, the conjugate gradient method will terminate at the solution in at most \(n\) iterations. When the distribution of the eigenvalues of \(H\) has certain favourable features, the algorithm will identify the solution in many fewer than \(n\) iterations.

If \(H\) has only \(r\) distinct eigenvalues, then the CG iteration will terminate at the solution in at most \(r\) iterations.

It is generally true that if the eigenvalues occur in \(r\) distinct clusters, the CG iterates will approximately solve the problem in about \(r\) steps.

Pre conditioned CG:

When the condition number \(\mathcal{K}\) of \(H\) is really high, then we run into issues. We introduce a technique called as pre-conditioning.

Here we transform the problem \(Hx = -c\) with the inverse of \(M\) where \(M\) is an SPD and invertible matrix, chosen by the user depending on the problem at hand:

We need: \(\mathcal{K}(M^{-1}H) \ll \mathcal{K}(H)\) or the eigenvalues of \(M^{-1}H\) are clustered together, thereby ensuring faster convergence to the actual solution in \(r\) steps, if there are \(r\) clusters.

Most of the standard solver packages use pre-conditioning for faster convergence.

Naive Code Implementation

The following class implements the reference Conjugate Gradient algorithm without preconditioning, for educational purposes only. Do not use it on your actual code!

import numpy as np

class quadratic_form:
    """
    Solve a linear system Hx = -c using a quadratic formulation.
    Uses the Conjugate Gradient method.
    """

    def __init__(self, H: np.ndarray, c: np.ndarray, rhs_sign: np.int64) -> None:
        """
        __init__: initialise the CG class.

        Input data = H, x, c.

        Parameters
        ----------
        H : np.ndarray
            System Matrix.
        c : np.ndarray
            rhs
        rhs_sign : np.int64
            Sign of rhs. If system is Hx = c, set rhs_sign = 1, else if Hx = - c, set rhs_sign = -1.
        """
        self.H = H
        self.c = c
        self.res_sgn = -rhs_sign
        self.rows, self.cols = H.shape

    def cgmin(
        self, x0: np.ndarray, maxiter: np.int64 = 2000, tol: np.float64 = 1.0e-8, debug: bool = False
    ) -> np.ndarray:
        """
        cgmin: Minimize positive definite quadratic form with conjugate gradient method.

        This routine uses the un-preconditioned efficient version of CG.

        Parameters
        ----------
        x0 : np.ndarray
            Initial Guess Vector

        maxiter : np.int64
            Maximum number of allowed iterations

        tol: np.float64
            Tolerance

        debug : bool
            Print iteration steps
        """
        x = x0  # initial guess
        r: np.ndarray = self.H @ x0 + self.res_sgn * self.c  # initial residual
        p: np.ndarray = -r  # initial direction
        i: np.int64 = 0

        rtr = r.T @ r
        while np.linalg.norm(r) > tol and i < maxiter:
            Hpi = self.H @ p
            alpha = rtr / (p.T @ Hpi)
            x = x + alpha * p
            r = r + alpha * Hpi
            rnr = r.T @ r
            if np.linalg.norm(r) < tol:
                break
            beta = rnr / rtr
            rtr = rnr
            p = -r + beta * p
            i += 1
            if debug:
                print(f"x is {x} at iteration #{i}")

        if i == maxiter:
            print("Max Iterations reached. Terminating procedure...")
            print(f"Error norm attained: {np.linalg.norm(r)}")
        else:
            print(f"Solution reached in {i} iterations.")
            print(f"Final Error Norm at solution: {np.linalg.norm(r)}")

        return x

The following sample code uses the above class to solve a symmetric positive-definite linear system:

A = 500 * np.random.randn(500, 500)
H = A.T @ A
c = 500 * np.random.randn(500)
x0 = np.ones(c.shape)

qform = quadratic_form(H, c, 1)
x = qform.cgmin(x0, maxiter=5000, tol=1e-8, debug=False)

print("Solution is :")
print(x)

Available Software

A high-quality, expert-developed Python implementation of the Conjugate Gradient method is available in the Scipy library as the scipy.sparse.linalg.cg function. See the documentation for more details.

Well engineered, high performance C language implementations of Conjugate Gradient are available in the Intel Math Kernel Library. The following links contain more information:

1. Iterative Sparse Solvers based on Reverse Communication Interface
2. CG Interface Description
3. dcg_init
4. dcg_check
5. dcg
6. dcg_get
7. Preconditioners based on Incomplete LU Factorization Technique

Non-Linear CG

If our objective function is not convex quadratic as we were dealing with till now, we will have to adapt our current way to fit it into a non-linear functions.

We were solving exactly for \(\alpha_k\) till now, but in the nonlinear case, we have to use the Backtracking line-search scheme to calculate \(\alpha\).

Instead of the residual \(r_k\), we will use \(\nabla f_k\), the gradient of the objective function at the current iterate.

\(\beta_{k+1}\) has to be recalculated in terms of \(\nabla f_k\) and the new search direction \(p_k\).

\(\beta_{k}\) can be calculated by the following update equations:

Fletcher - Reeves Method

Polak Ribere Method:

Hestenes-Steifel Method:

References

1. An Introduction to the Conjugate Gradient Method Without the Agonizing Pain
2. Nocedal and Wright, Numerical Optimization
3. Trefethen and Bau, Numerical Linear Algebra
4. David C. Lay, Linear Algebra and Its Applications
5. Gilbert Strang, Introduction to Linear Algebra
6. Chapra and Canale, Numerical Methods for Engineers
7. The Wrong Iterative Method: Steepest Descent